Our galaxy has a diameter a
a of around 100,000 light years. The average thickness h,
the disk, is 3,000 light years. This is also where most of the stars are.
The center, roughly in the shape of a sphere, has a diameter d
of 16,000 light years. The volume of the galaxy is approximately:
V = Vsphere
+ Vcylinder
– Vsphere cutout
V = p/6 · d3 + p · a2/4 · h
– p · d2/4 · h
V = p/6 · 160003 + p · 100.0002/4 · 3000 – p ·
16.0002/4 · 3000
V = 2,510.341.97·1013
Ly3
If you take the space that the galaxy occupies and convert it into a cube, you get:
V = a3
If this space is also occupied by a number N of stars, then the result is:
V = a3
· N
Then the average distance
between two stars is:
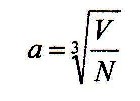
Our galaxy has around 100 to 300 billion suns.
There is an average distance of 4.37 to 6.3 light years between the individual stars.
For comparison: Alpha Centauri, our nearest neighbor sun, is 4.24 light-years away.
This type of averaging, through the formation of cubes, is required for further
considerations in order to be able to convert planetary frequencies into medium
distances. Due to the formation of cubes, the average distances between the
stars appear directly as edges of the cubes belonging to the suns.
The cube approach allows a relatively simple calculation of an “average distance”,
which would be much more difficult with a cylinder or a sphere. When they are
lined up next to each other, empty spaces are created that cannot be calculated,
while cubes can be lined up seamlessly.
|